Zlatý řez
Autor: Vojtěch AloyVydáno: 21. 12. 2022 12:00
V tomto příspěvku se věnuji Fibonacciho posloupnosti a zlatému řezu.
Fibonacciho posloupnost
Fibonacciho posloupnost je v matematice nekonečná řada čísel. Začíná takto: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, a tak dále.
Definice funkce je F(n) = {0 pro n = 0; 1 pro n = 1; F(n-1) + F(n-2)}
Zajímavé na Fibonacciho posloupnosti je to, že poměr dvou čísel, která leží v řadě vedle sebe, se limitně blíží zlatému řezu (přibližně 1 : 0,618). Tento jev ilustruji v přiložené tabulce.
| n | F(n) | F(n+1) | Poměr |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 |
| 3 | 2 | 3 | 0,66666667 |
| 4 | 3 | 5 | 0,6 |
| 5 | 5 | 8 | 0,625 |
| 6 | 8 | 13 | 0,61538462 |
| 7 | 13 | 21 | 0,61904762 |
| 8 | 21 | 34 | 0,61764706 |
| 9 | 34 | 55 | 0,61818182 |
| 10 | 55 | 89 | 0,61797753 |
| 11 | 89 | 144 | 0,61805556 |
Zlatý řez
Zlatý řez je sám o sobě definovaný jako rozdělení úsečky na dve části tak, aby poměr větší části k celé úsečce byl stejně velký, jako poměr menší úsečky k větší úsečce.

Platí tedy, že |AC| : |AB| = |CB| : |AC|
Tento poměr je roven iracionálnímu číslu - zlatému řezu.
Zlatý řez se často zobrazuje graficky také v podobě takzvané zlaté spirály. Stejně jako v případě úsečky zde platí, že čtvrtiny kružnice se zmenšují v poměru zlatého řezu.
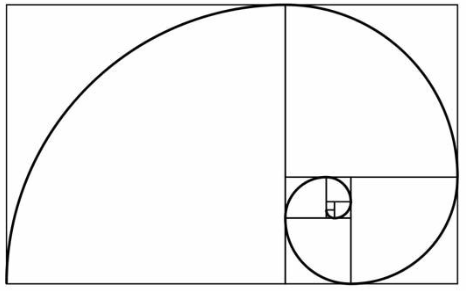
Výskyt v přírodě
V reálném světě se objevuje poměr fibonacciho posloupnosti velmi často, zejména v podobě logaritmické (zlaté) spirály. Například šupiny šišky smrku jsou rozmístěny do spirály. Z živočichů nelze nejmenovat hlemýždě a obecně další plže s úlitou. Hmyz, který se blíží k lampě se velmi často pohybuje právě po logaritmické spirále.
Využití
Zlatý řez se využívá zejména v oblasti umění. Mnoho obrazů má hlavní motiv umístěný právě ve zlatém řezu. Toto pravidlo je často využíváno také fotografy.